Figure 1. NFA for Regex Pattern “(ca*t|lion)+.*(dog)?”

I came across a problem on leetcode a few days ago. It asked me to implement a simple regex (regular expression) matcher which supports both . and * qualifiers. A brute force algorithm for this simple case alone could end up an exponential time efficiency, not to mention if it were to support all basic regex operators, i.e. ., *, +, ?, | and (). However, we could use a Non-deterministic Finite Automata (NFA) technique to make the matcher run in linear time efficiency. By doing that, both NFA construction and string testing on NFA will be linear time. Another benefit is that once a pattern is compiled to a NFA, that NFA can be used to test all future strings for that pattern without recompile the pattern every time. Appealing enough? Right, let’s start by first seeing how this NFA approach works, then I will show you my Python code, which constructs a NFA for a given pattern, tests the constructed NFA on arbitrary strings, and draws the NFA out beautifully to a PDF file (like the one shown above).

Regex Syntax

. matches any single character
* matches zero or more of the preceding element
+ matches one or more of the preceding element
? matches zero or 1 of the preceding element
| matches the preceding element or following element
() groups a sequence of elements into one element

The matching covers the entire input string (not partial).

The NFA Algorithm

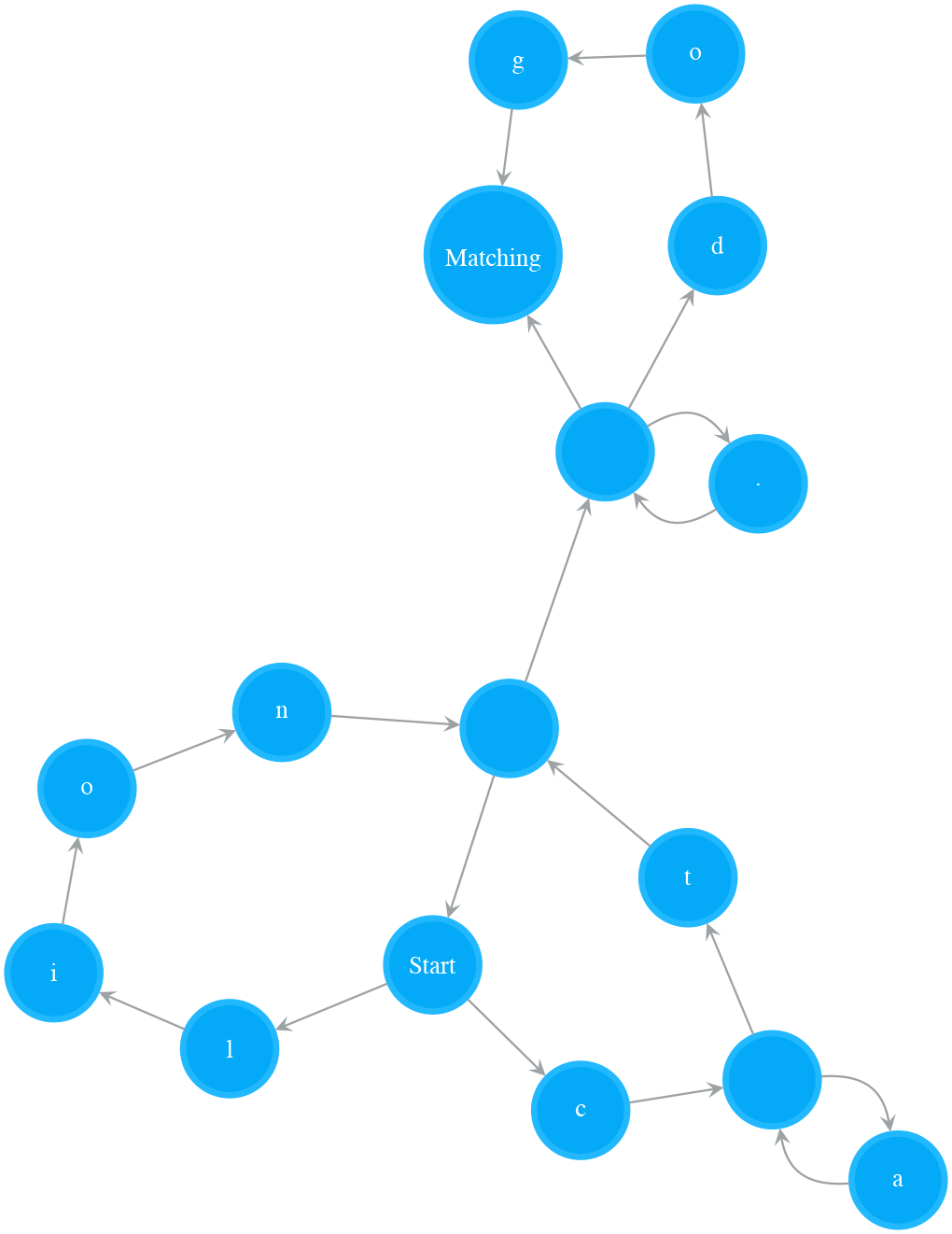
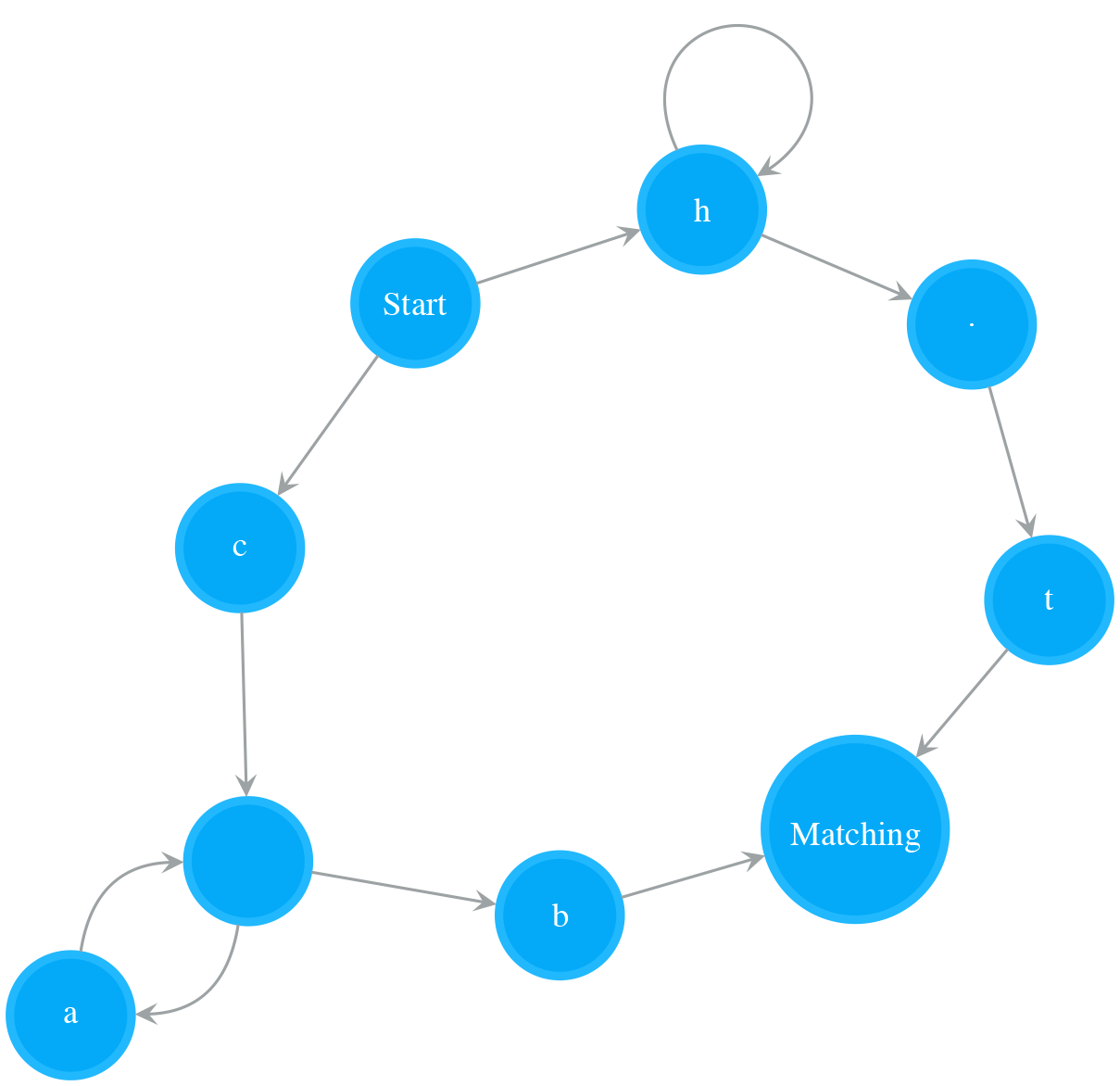
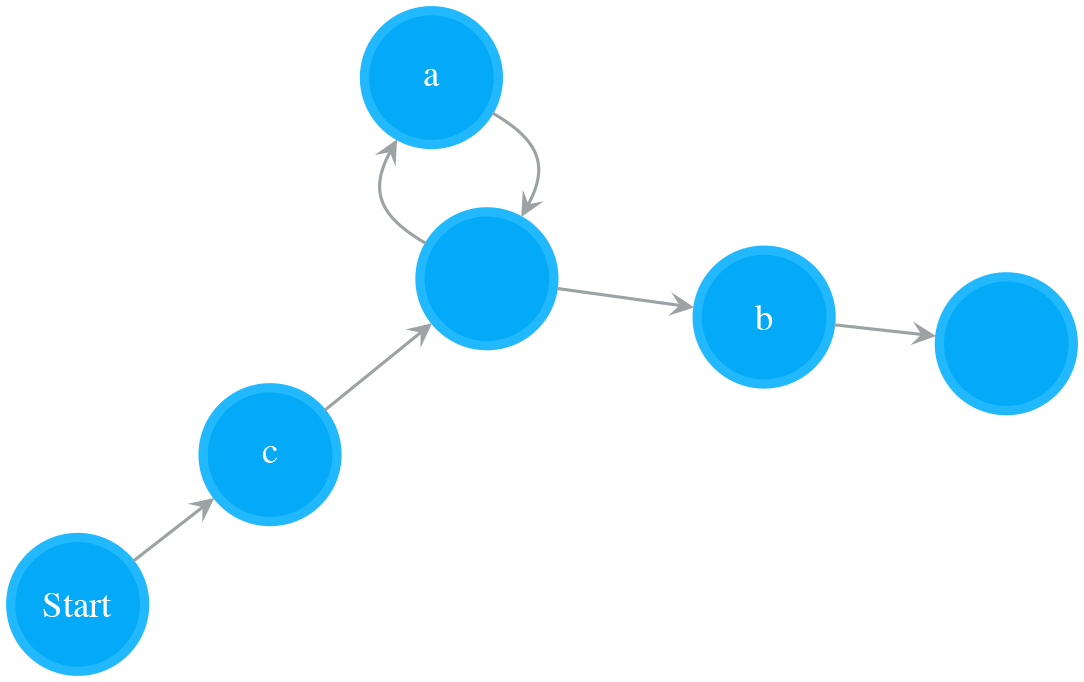
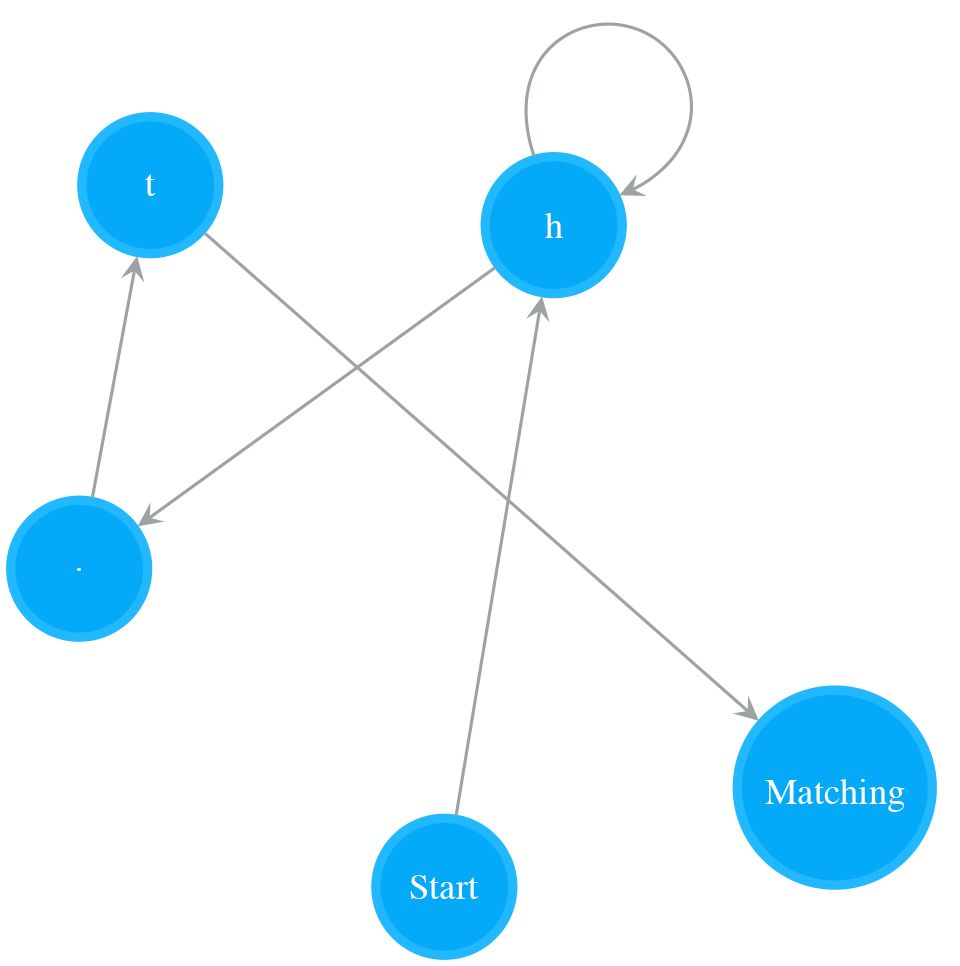
Every regex pattern has a corresponding NFA. In order to test the matching between a string and a pattern, we can build a NFA for that pattern and run the string on the NFA to make the decision. Say, if our testing string is “catsdog” and pattern is “(cat|lion)+.(dog)?”, we can build a NFA showing in Figure 1, then test the string “catsdog” on it. Let’s first see how this works.

Testing String on NFA

We keep track of NFA’s current states in a set cur_states

1. Initialise the NFA by putting the Start state in cur_states
2. Remove a character char from left of the testing string
3. For every state in cur_states, first remove it from the set, then check to see whether it can consume the given character char or not:
   1. If it is a normal state (a State with an enclosed character), check whether char is equal to the normal state’s char or the normal state is a ‘.’ state (a ‘.’ state can match any character):
      1. If yes, the char can be consumed by this neighbour state. Add its outgoing neighbours to cur_states
      2. If no, do nothing
   2. If it is a special state (either a Start, Empty or Matching state), go check the special state’s outgoing neighbours and repeat the same process until reach normal states, then rewind to previous step. Special states consume nothing.
4. Rewind to step 2 and keep doing the same process until either cur_states becomes empty or all characters in the testing string have been removed. In the former case, return False
5. Check whether cur_states contains the Matching state or from those states in cur_states whether they can reach the Matching state (via Special states). If either case is true, return True; otherwise return False

Testing String “catsdog” on NFA “(ca*t|lion)+.*(dog)?”

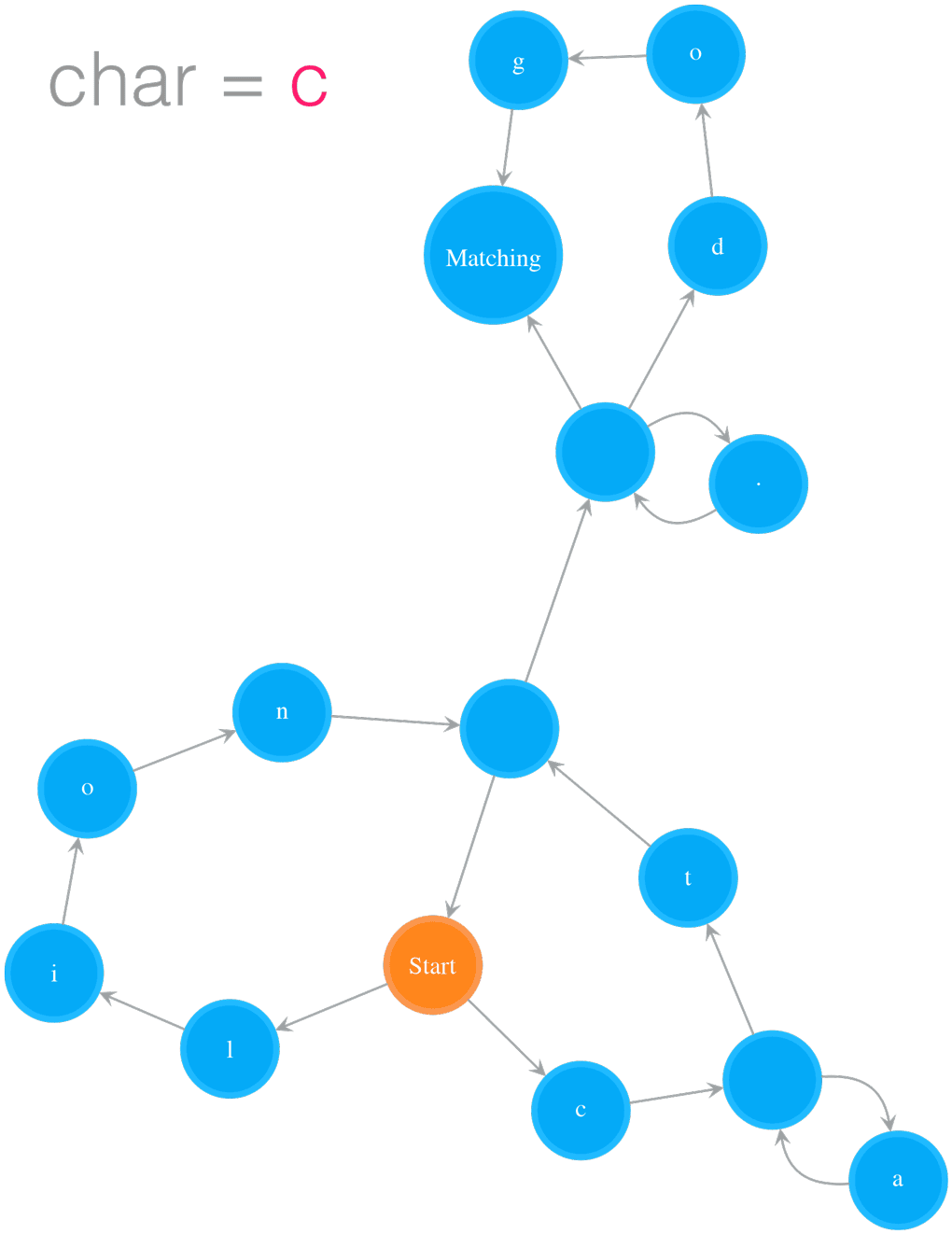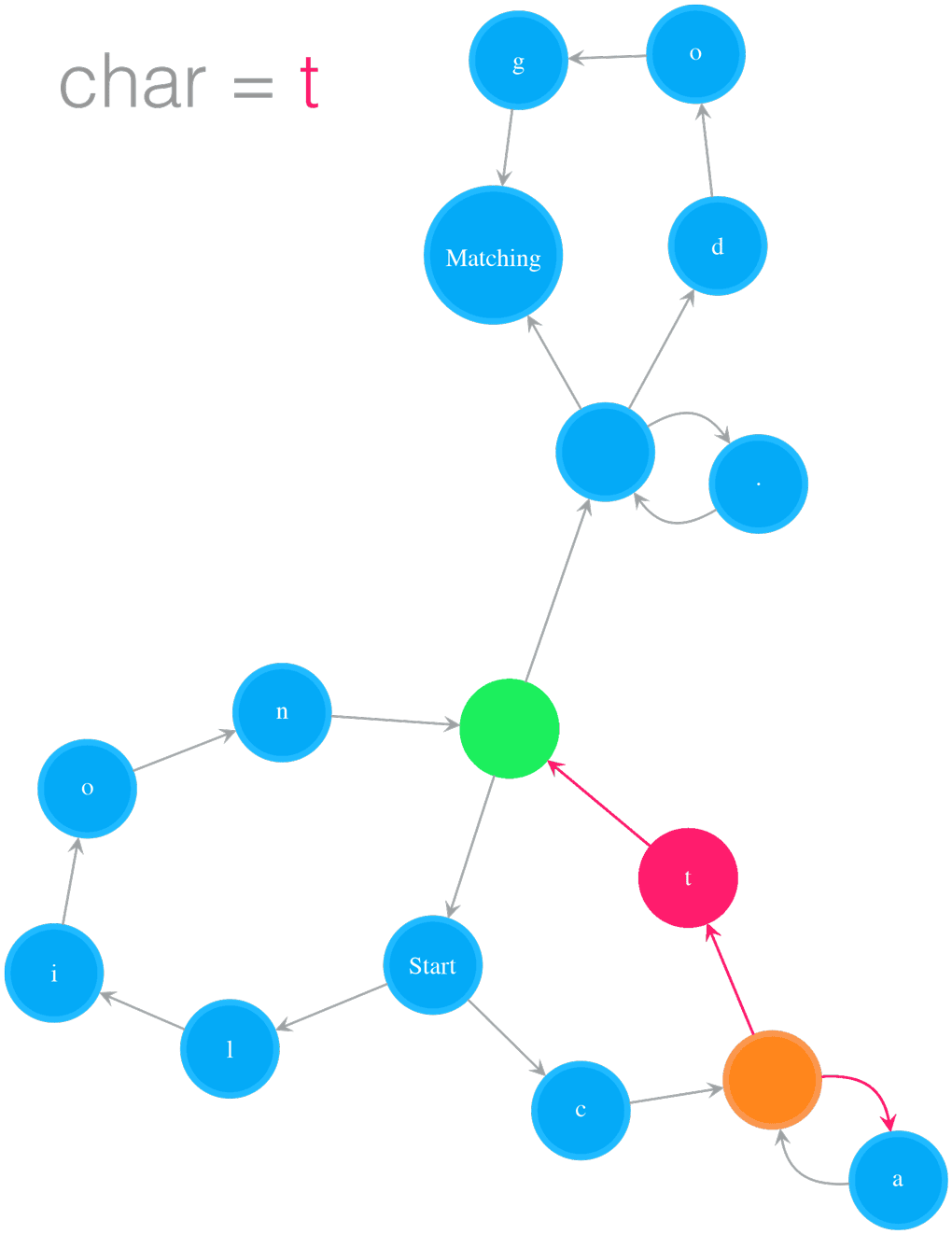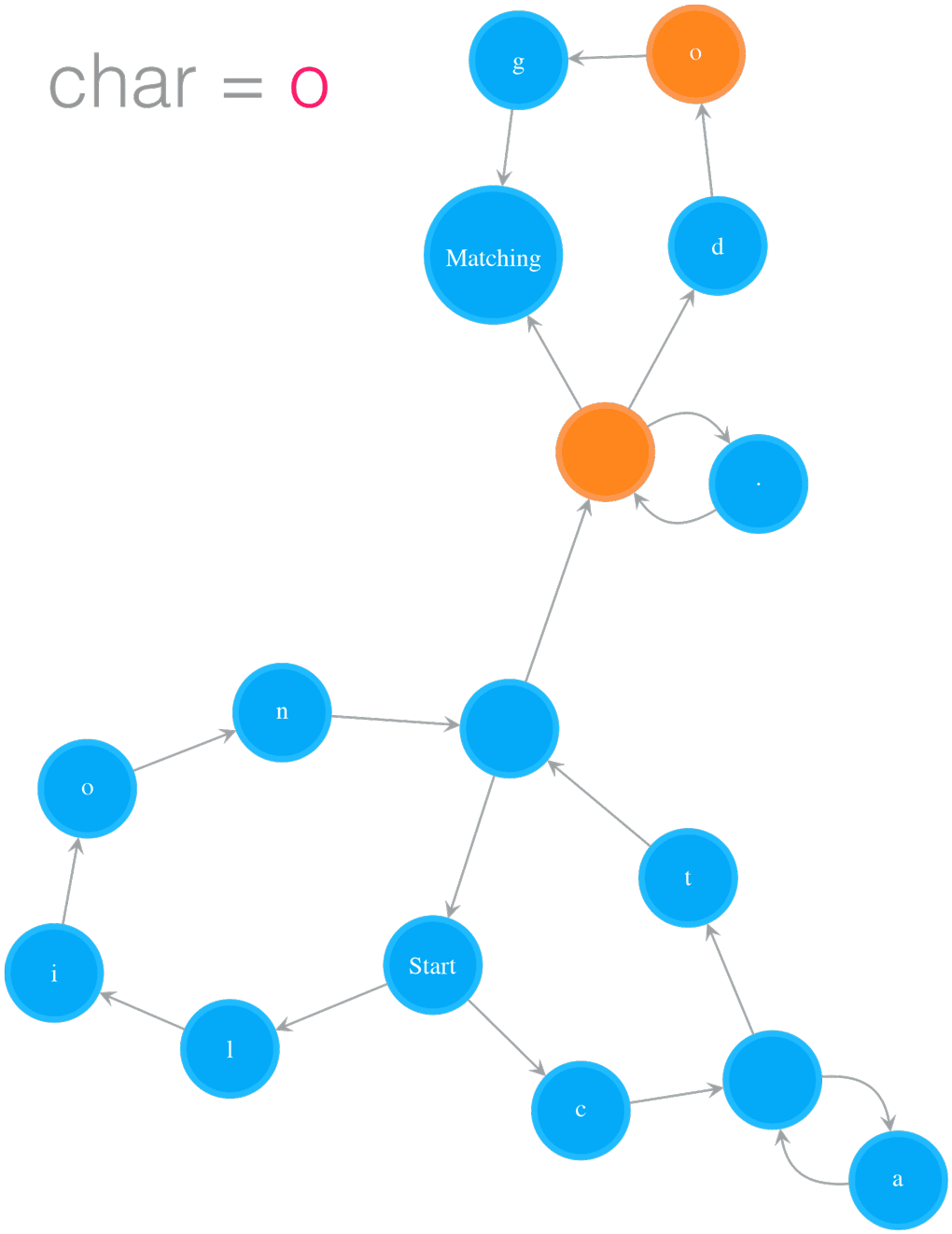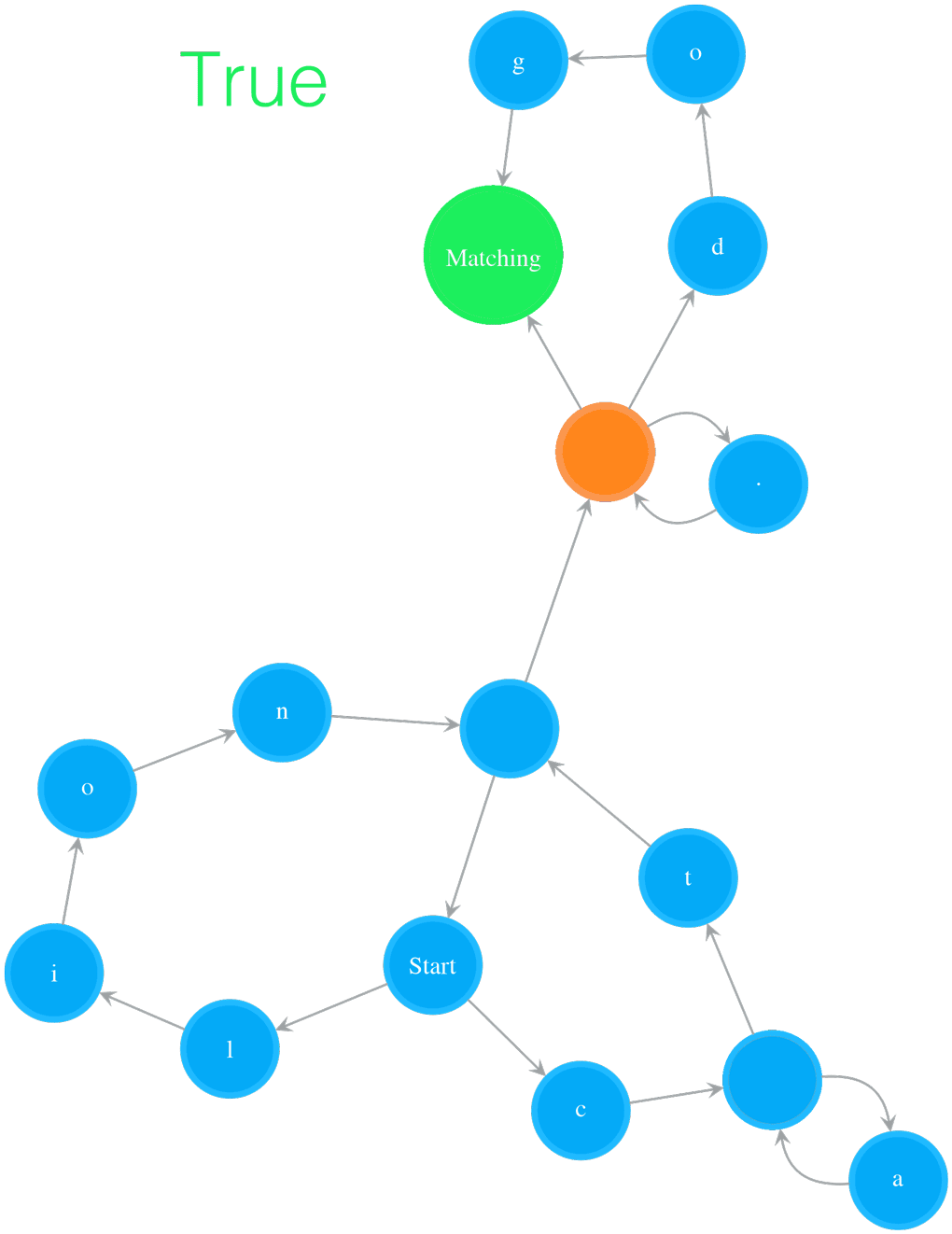
Figure 2. Testing String “catsdog” on NFA “(ca*t|lion)+.*(dog)?”

The example in Figure 2 illustrates how to test the string “catsdog” on the NFA of pattern “(cat|lion)+.(dog)?”. The orange colour states are the states in cur_states, which means the states the NFA is currently in. In order for the NFA to move to next set of states, it needs to check those states in cur_states. In the example, the NFA starts at Start state, and checks whether the Start state can consume current char, i.e. ‘c’, or not. Because the Start state is a special state that consumes nothing, the NFA passes it and checks its outgoing neighbours, i.e. ‘l’ and ‘c’ states. The ‘l’ state cannot consume ‘c’, so we stop exploration on that path. The ‘c’ state can consume ‘c’, we add its outgoing neighbour, an Empty state, to cur_states. Now the NFA is in states cur_states, which equals to set([Empty state]). Then the next round starts at the Empty state, and the same process keeps going on. The NFA moves to next, further next and so on set of states while it consumes characters. After the NFA has consumed all the characters in “catsdog”, it is in cur_states = set([Matching state, Empty state]), i.e. the Matching state and the Empty state before the Matching state. Because the Matching state is in this final cur_states, the matching succeeds, and therefore we return True.

In terms of time efficiency, the NFA scans the test string once. In the worst case, the NFA might be in all available states at each step, but this results in at worst a constant amount of work independent of the length of the string, so arbitrarily large input strings can be processed in linear time O(n). If it were using different patterns to test strings, the overall time efficiency of this NFA approach is O(m*n), where the m and n is the length of pattern and test string respectively.

Next, let’s see how we can compile a given pattern into a NFA.

Compile Pattern into NFA

The most interesting thing about NFA is that we can use a NFA as a building block for a larger NFA. Let’s first consider the following simple cases:

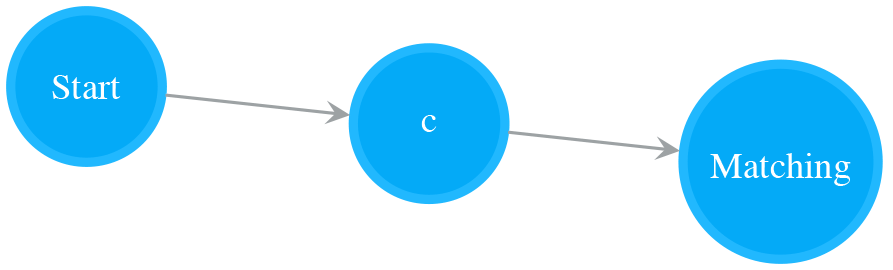
NFA for a Single Character

A NFA of a single Normal state matches a single character. The following NFA matches “c”.

 

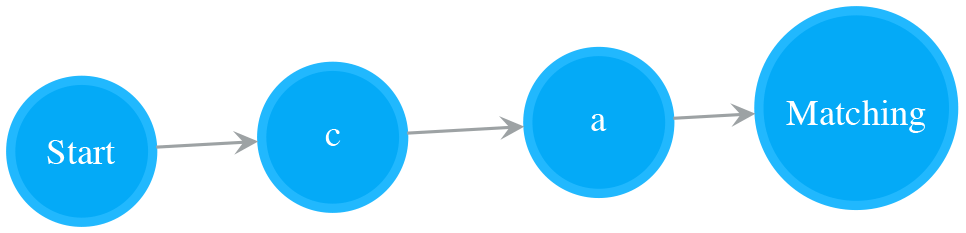
Put Two NFAs in Serial (Concatenation)

A NFA of two Normal states in serial matches the character sequence. The following NFA is a serial combination of NFA for “c” and NFA for “a”. It matches “ca”.

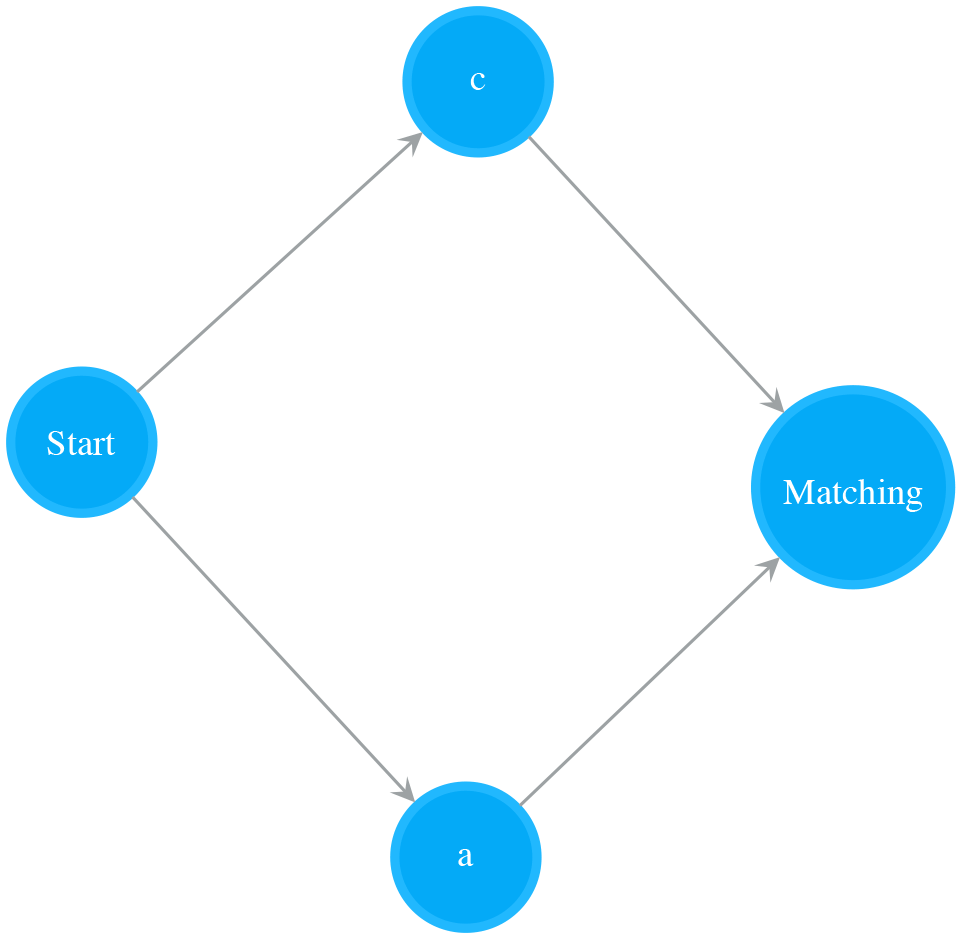
Put Two NFAs in Parallel (|)

A NFA of two Normal states in parallel matches the character alternation. The following NFA is a parallel combination of NFA for “c” and NFA for “a”. It matches “c|a”, i.e. “c” or “a”.

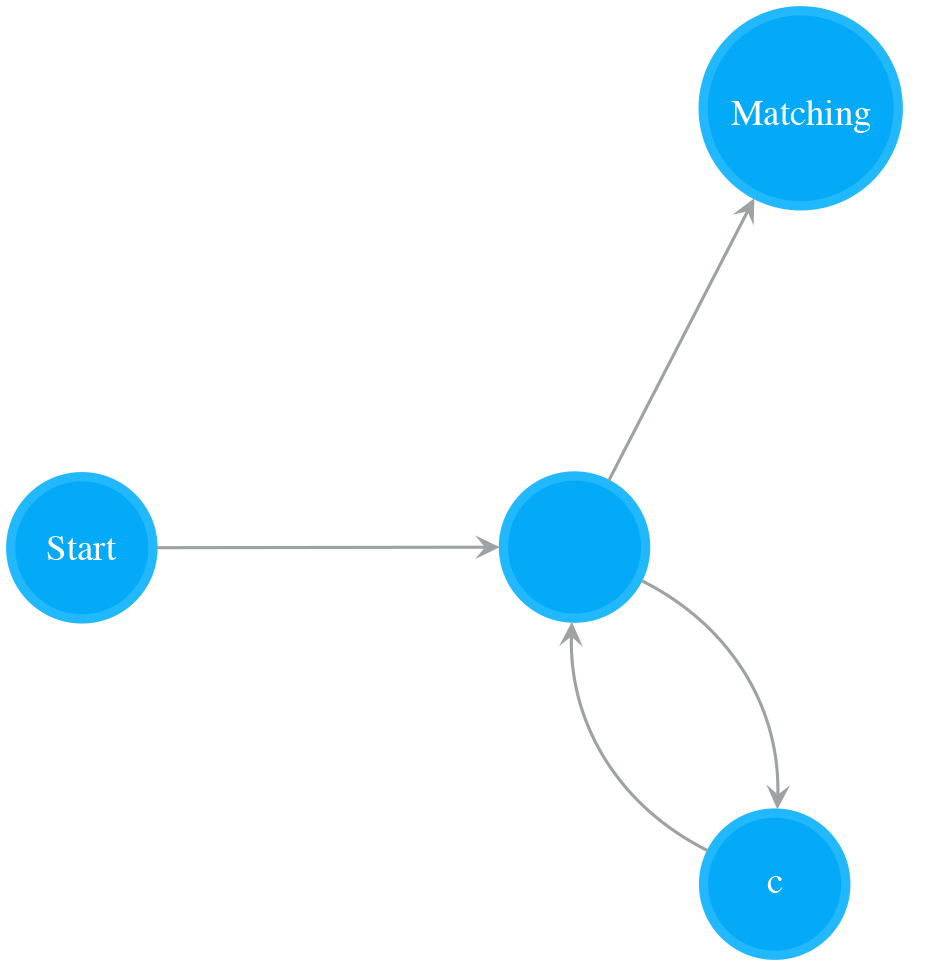
Repeat Zero or More Times (*)

A NFA of an Empty state and a Normal state attached on the Empty state matches zero or more times of a single character. The following NFA is a result of attaching a Normal state on Empty NFA (matches empty string). It matches “c*”, i.e. “”, “c”, “cc”, “ccc…”.

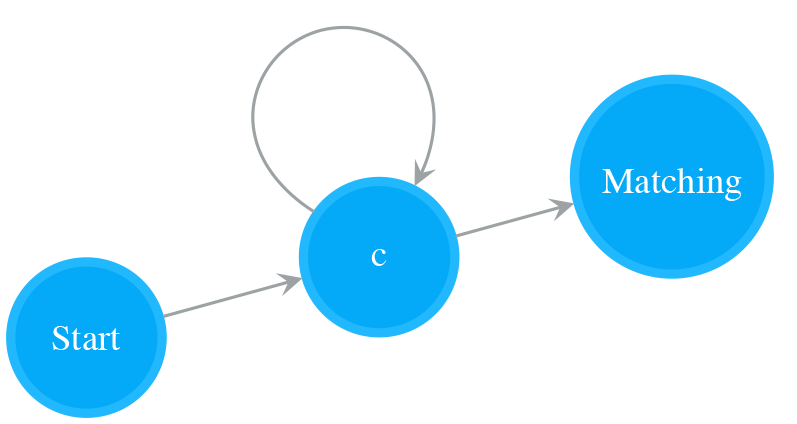
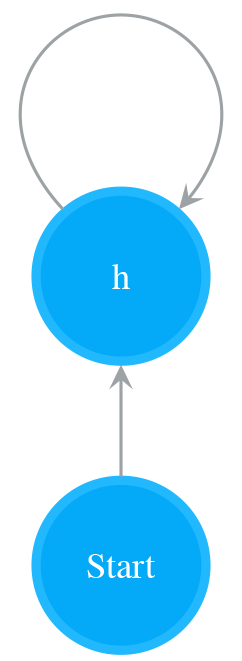
Repeat One or More Times

A NFA of a single Normal state with a self-loop matches one or more times of a single character. The following NFA is a result of adding a self-loop to the Normal state of NFA for “c”. It matches “c+”, i.e. “c”, “cc”, “ccc…”.

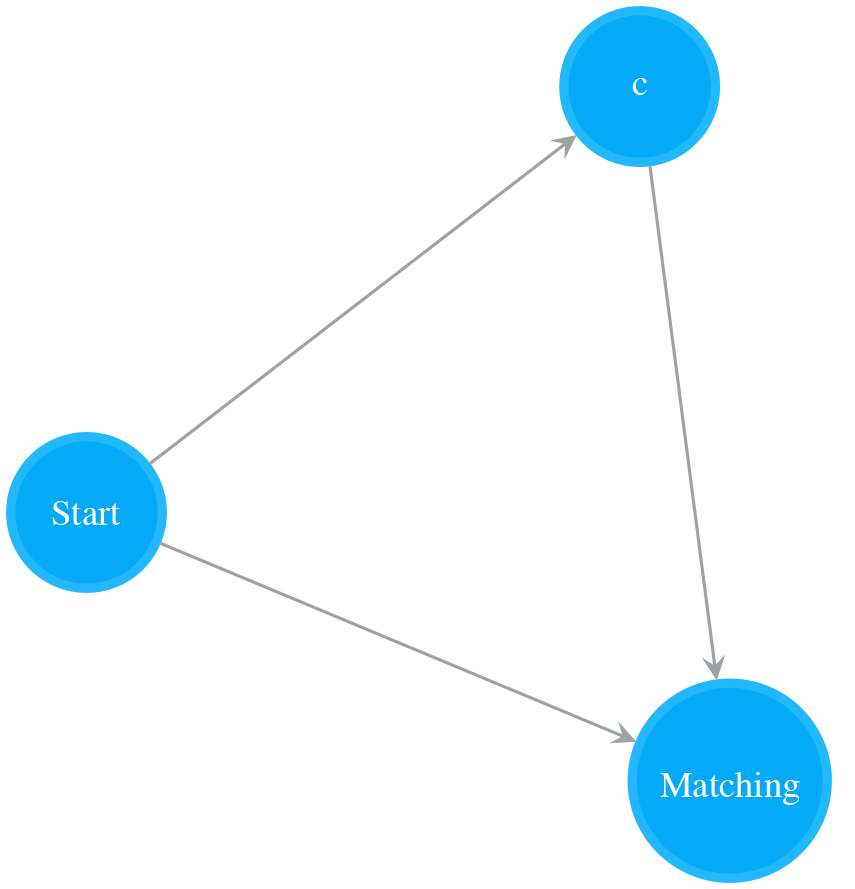
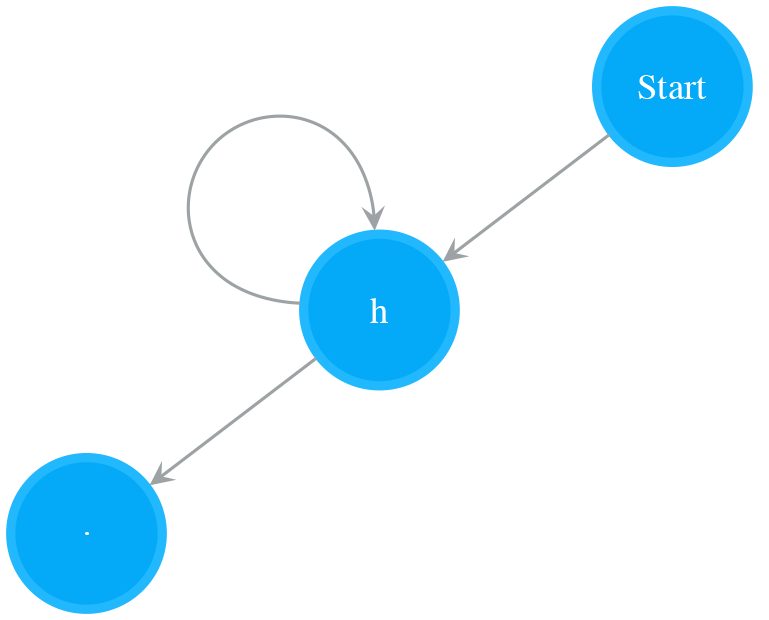
Optional

A NFA of a single Normal state with Start state connecting to its Matching state optionally matches a single character. The following NFA is NFA for “c” connecting its Start and Matching state. It matches “c?”, i.e. “” or “c”.

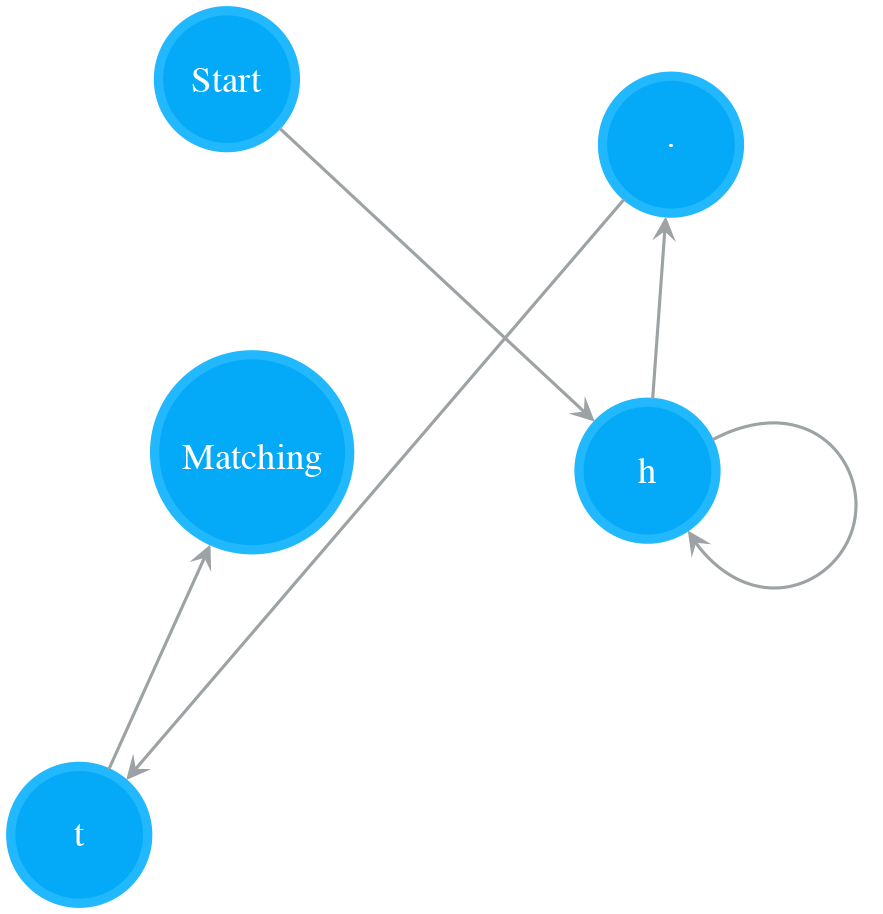
Treat a NFA as if It were a Single Character ((), parenthesis)

We can group a sequence of regex pattern characters in parenthesis, and treat them as if it were a single character. Then we can make use of all the basic NFA building blocks presented above to build more complex NFAs. For example, we can group regex pattern “cab” and “h+.t” in parenthesis, and put them in parallel like this “(cab)|(h+.t)”. This results in the following complex NFA to match strings like “cab”,  “hut” or “caaaab”.

The Regex Pattern Parser/Compiler

With the above basic building blocks, the compilation of a regex pattern to a NFA becomes easy. Basically, we can write a parser to linearly scan through a given regex pattern and add sub-NFAs one by one. During the parsing, we need to temporally store the previous operand (a sub-NFA) for the next operator (one of the above building blocks) to use.

To demonstrate the idea, we can parse and compile the pattern “(ca*b)|(h+.t)” in previous example as follows:

1. Start a new NFA nfa with a Start state, and create a variable last_operand
   

   

   nfa

2. Read “(“. Start another NFA nfa_sub  (a sub-NFA), and create a variable last_operand_1
   

   

   nfa

   

   nfa_sub

3. Read “c”. Construct NFA for “c” and store it to last_operand_1

   

   nfa

   

   nfa_sub

4. Read “a”. Append last_operand_1 to nfa_sub, construct NFA for “a” and store it to last_operand_1

   

   nfa

   

   nfa_sub

5. Read “*”. Treat last_operand_1 as a single character, repeat last_operand_1 zero or more times, and append the result NFA to nfa_sub

   

   nfa

   

   nfa_sub

6. Read “b”. Construct NFA for “b” and store it to last_operand_1

   

   nfa

   

   nfa_sub

7. Read “)”. Append last_operand_1 to nfa_sub, attach a Matching state to nfa_sub to make it a complete NFA and store nfa_sub to last_operand

   

   nfa

   

   last_operand = nfa_sub

8. Read “|”. Append last_operand to nfa, start another NFA nfa_sub_1, and create a variable last_operand_2

   

   nfa

   

   nfa_sub_1

9. Read “(“. Start another NFA nfa_sub_2, and create a variable last_operand_3
   

   

   nfa

   

   nfa_sub_1

   

   nfa_sub_2

10. Read “h”. Construct NFA for “h” and store it to last_operand_3

    

    nfa

    

    nfa_sub_1

    

    nfa_sub_2

11. Read “+”. Treat last_operand_3 as a single character, repeat last_operand_3 one or more times, and append the result NFA to nfa_sub_2

    

    nfa

    

    nfa_sub_1

    

    nfa_sub_2

12. Read “.”. Construct NFA for “.” and store it to last_operand_3

    

    nfa

    

    nfa_sub_1

    

    nfa_sub_2

13. Read “t”. Append last_operand_3 to nfa_sub_2, construct NFA for “t” and store it to last_operand_3

    

    nfa

    

    nfa_sub_1

    

    nfa_sub_2

14. Read “)”. Append last_operand_3 to nfa_sub_2, attach a Matching state to nfa_sub_2 to make it a complete NFA and store nfa_sub_2 to last_operand_2.

    

    nfa

    

    nfa_sub_1

    

    last_operand_2 = nfa_sub_2

15. Append last_operand_2 to nfa_sub_1, attach a Matching state to nfa_sub_1 to make it a complete NFA and store nfa_sub_1 to last_operand_1.

    

    nfa

    

    last_operand_1 = nfa_sub_1

16. Put last_operand_1 and nfa in parallel, attach a Matching state to nfa to make it a complete NFA. Then nfa is the final NFA for pattern “(ca*b)|(h+.t)”

    

    Final NFA

As you might have seen,  some simplification works for the merged NFA graphs had been done implicitly in the above example. Due to the length of this documentation, I will not explain any further. Welcome to read the comments in my code if you would like to know more.

Since we only need to scan the pattern string once in order to build the corresponding NFA, the time efficiency for this step is linear O(n) as well.

My Python Implementation

I have implemented this NFA algorithm in Python. It supports all basic regex operations shown in this documentation. Apart from compiling given patterns to NFAs and matching strings on those NFAs, it also supports drawing out those NFAs beautifully to PDF files. As you can see, all my figures in this documentation are drawn using it.

Download

You can download and try it yourself using the following link:

Download regex_matching.py   2722 hits

I wrote this mainly for educational purpose, but you are free to modify it in any way. If you like it, please consider making a small donation to me via PayPal as to show your thanks and support for my work

If you have any question, please post a comment. I will try my best to answer it.

Below is some help information that you may find useful.

Usage

General syntax:

Match string “catsdog” against pattern “(cat|lion)+.(dog)?” and draw internal NFA to ‘NFA.pdf’ (requires graph-tool):

Match string “catsdog” against pattern “(cat|lion)+.(dog)?” and draw the internal NFA at every step to ‘NFA.pdf’ (requires graph_tool; It is best to run this option and observe the result with a PDF viewer that can detect file change and reload the changed file. For example, the Skim app):

Match string “catsdog” against pattern “(cat|lion)+.(dog)?”:

Run built-in test cases:

Show help message:

Further Readings

Regular Expression Matching Can Be Simple And Fast: http://swtch.com/~rsc/regexp/regexp1.html
An Efficient and Elegant Regular Expression Matcher in Python: http://morepypy.blogspot.com.au/2010/05/efficient-and-elegant-regular.html